前言
在處理文件結構時（例如 Word 文件、Markdown 目錄、HTML 標題），我們常遇到一個挑戰：如何從按順序排列的扁平標題清單（Heading 1/2/3）快速找出每個標題的「父標題」位置，進而建立完整的樹狀結構？
本文將介紹一個 O(n) 時間複雜度的堆疊（Stack）演算法，只需單次遍歷即可完成父子索引對應，適用於任意深度的階層結構。
問題定義
輸入
一份按文件順序排列的標題清單，每個標題包含：
編號（例如：1, 1.1, 1.2, 2, 2.1）
層級（level）：1 = Heading 1，2 = Heading 2，3 = Heading 3
標題文字（title）
輸出
為每個標題計算：
parent_index：父標題在清單中的索引（None 代表頂層標題）
children_count：直接子標題數量（初始化為 0）
範例
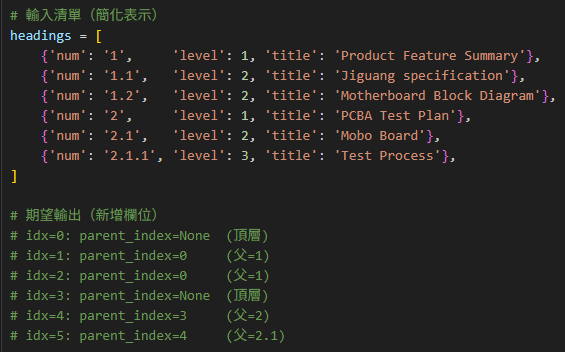
# 輸入清單（簡化表示）
headings = [
{'num': '1', 'level': 1, 'title': 'Product Feature Summary'},
{'num': '1.1', 'level': 2, 'title': 'Jiguang specification'},
{'num': '1.2', 'level': 2, 'title': 'Motherboard Block Diagram'},
{'num': '2', 'level': 1, 'title': 'PCBA Test Plan'},
{'num': '2.1', 'level': 2, 'title': 'Mobo Board'},
{'num': '2.1.1', 'level': 3, 'title': 'Test Process'},
]
# 期望輸出
# idx=0 (標題號=1): parent_index=None → 頂層標題
# idx=1 (標題號=1.1): parent_index=0 → 父標題是 headings[0]，即編號 1
# idx=2 (標題號=1.2): parent_index=0 → 父標題是 headings[0]，即編號 1
# idx=3 (標題號=2): parent_index=None → 頂層標題
# idx=4 (標題號=2.1): parent_index=3 → 父標題是 headings[3]，即編號 2
# idx=5 (標題號=2.1.1): parent_index=4 → 父標題是 headings[4]，即編號 2.1核心演算法：堆疊追蹤祖先鏈
關鍵洞察
- 父標題必定出現在子標題之前（文件順序特性）
- 父標題的層級必定小於子標題（1 < 2 < 3）
- 遇到同級或更淺層級時，需「回退」到合適的祖先
堆疊結構
stack: List[Tuple[int, int]] = []
# (heading_level, idx_in_headings)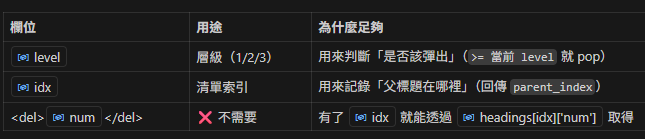
用途：維護「目前可能成為後續標題父節點」的候選清單
元素格式：(層級, 索引)
性質：堆疊由淺到深排列（level 遞增）
完整程式碼
from typing import List, Tuple
def build_parent_child_relations(headings: List[dict]) -> None:
"""
為標題清單建立父子關係（原地修改）。
Args:
headings: 標題清單，每個元素必須包含 'level' 欄位
Modifies:
為每個標題新增 'parent_index' 與 'children_count' 欄位
Time Complexity: O(n)
Space Complexity: O(d)，d 為最大深度
"""
# 堆疊：儲存 (層級, 索引)
stack: List[Tuple[int, int]] = []
for idx, h in enumerate(headings):
lvl = h['level']
parent_idx = None
if lvl is not None:
# 關鍵步驟：移除所有「層級 ≥ 當前層級」的祖先
while stack and stack[-1][0] >= lvl:
stack.pop()
# 如果堆疊非空，頂端元素即為父標題
if stack:
parent_idx = stack[-1][1]
# 將當前標題加入堆疊（可能成為後續標題的父節點）
stack.append((lvl, idx))
# 記錄結果
h['parent_index'] = parent_idx
h['children_count'] = 0 # 初始化，稍後統計核心邏輯：「最近合法祖先」追蹤器
比喻：爬山找庇護所
想像你在爬一座有多個層級的山：
Level 1：山腳大本營（Heading 1）
Level 2：半山腰營地（Heading 2）
Level 3：山頂小屋（Heading 3）
你按順序拜訪每個地點，每次到新地點時：
往回看：哪個「比我低的地點」最近？那就是我的「上級庇護所」（父標題）
記錄：我是從哪個庇護所來的
標記：我也可能成為後面人的庇護所（加入候選名單）
三個關鍵問題
- 為什麼需要「堆疊」？
問題情境：
你遇到這樣的標題順序：
1 (山腳)
1.1 (半山腰A)
1.1.1 (山頂小屋)
1.2 (半山腰B) ← 這裡！當你到達 1.2 時：
前一個地點是 1.1.1（山頂小屋）
但 1.2 不應該把 1.1.1 當父標題（太深了！）
真正的父標題是 1（山腳大本營）
解法：用堆疊記住「每個高度最後一個庇護所」
到達 1.2 時：
堆疊裡有：[1(山腳), 1.1(半山腰), 1.1.1(山頂)]
發現「1.1.1 太高了」→ 丟掉
發現「1.1 也一樣高」→ 丟掉
只剩「1(山腳)」→ 這才是我的父標題！- 什麼時候要「清理堆疊」？
規則：遇到「同高度或更低的地方」時，丟掉所有「比我高或同高」的候選。
為什麼？
如果你從山頂（level 3）下到半山腰（level 2），山頂的庇護所不再是「最近的上級」
你需要回到「比半山腰更低」的地方去找父標題
具體動作：
當前 level = 2，堆疊 = [(1, idx_A), (2, idx_B), (3, idx_C)]
↑保留 ↑丟掉 ↑丟掉
while 堆疊頂的 level >= 2:
pop! # 丟掉所有 ≥ 2 的
結果：堆疊 = [(1, idx_A)] # 只留比 2 低的- 如何找到「父標題」？
答案：清理完堆疊後，堆疊頂端就是最近的合法父標題。
為什麼是堆疊頂？
堆疊由淺到深排列：[level 1, level 2, level 3, …]
清理掉「太高的」後，最上面那個就是「最接近的低層」
這就是「最近合法祖先」
範例：
到達 1.2 (level 2)
堆疊 = [(1, idx_0)] # 只剩 level 1
父標題 = stack[-1] = (1, idx_0)
→ 所以 1.2 的 parent_index = idx_0 (指向標題 "1")完整邏輯流程（人話版）
Step by Step
1. 初始化：準備一個空的「候選庇護所名單」（堆疊）
2. 依序拜訪每個標題：
對於每個標題 X：3. 清理名單：
檢查名單最後一個候選：
- 如果它「跟我一樣高或更高」→ 丟掉！（它不能當我的上級）
- 重複檢查，直到名單是空的，或者找到一個「比我低的」4. 找父標題：
如果名單還有候選 → 最後一個就是我的父標題
如果名單空了 → 我是頂層標題（沒有父親）5. 登記自己：
把我自己加進名單（我可能成為後面人的父標題）6. 記錄結果：
把「我的父標題是誰」寫下來為什麼這樣做是正確的？
保證 1：父標題一定在前面
文件是順序掃描的（1 → 1.1 → 1.2 → 2）
父標題一定比子標題先出現
保證 2：父標題層級一定更淺
Level 1 才能當 Level 2 的父親
清理掉「太高的」保證這一點
保證 3：找到最近的父標題
堆疊維持「由淺到深」順序
清理後，堆疊頂 = 最接近的合法父親
用故事總結
你是一個探險家，按順序拜訪山上的營地：
1. 到達「山腳 1 號營地」(level 1)
→ 沒有上級，記錄「我是頂層」
→ 把自己加入「可能的上級名單」
2. 到達「半山腰 1.1 號營地」(level 2)
→ 檢查名單：「山腳 1 號」比我低 ✓
→ 記錄「我的上級是山腳 1 號」
→ 把自己加入名單
3. 到達「山頂 1.1.1 號小屋」(level 3)
→ 檢查名單：「半山腰 1.1」比我低 ✓
→ 記錄「我的上級是半山腰 1.1」
→ 把自己加入名單
4. 到達「半山腰 1.2 號營地」(level 2) ← 關鍵！
→ 檢查名單：
- 「山頂 1.1.1」(level 3) ≥ 我 (level 2) → 丟掉！
- 「半山腰 1.1」(level 2) ≥ 我 (level 2) → 也丟掉！
- 「山腳 1 號」(level 1) < 我 ✓ 保留
→ 記錄「我的上級是山腳 1 號」
→ 把自己加入名單
5. 到達「山腳 2 號營地」(level 1)
→ 檢查名單：全部都 ≥ 1 → 全部丟掉！
→ 名單空了 → 記錄「我是頂層」
→ 把自己加入名單關鍵洞察
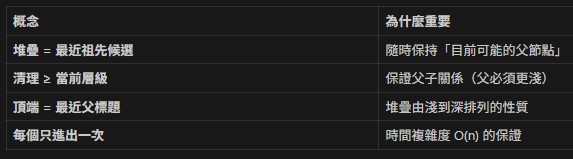
一句話總結
用堆疊維護「由淺到深的祖先鏈」，
遇到新標題時先丟掉「太高的候選」，
剩下的堆疊頂就是最近的合法父標題。
現在再看程式碼，每一行都是在實現這個邏輯：
while stack and stack[-1][0] >= lvl:→ 清理太高的if stack: parent_idx = stack[-1][1]→ 找最近父親stack.append((lvl, idx))→ 登記自己
headings如:
[{'start': 31,
'raw': '1\tProduct Feature Summary',
'style': 'Heading 1',
'end': 32,
'level': 1,
'number_text': '1',
'title': 'Product Feature Summary',
'slug': 'product-feature-summary',
'parent_index': None,
'children_count': 2,
'full_number_path': '1'},
{'start': 32,
'raw': '1.1 Jiguang specification',
'style': 'Heading 2',
'end': 35,
'level': 2,
'number_text': '1.1',
'title': 'Jiguang specification',
'slug': 'jiguang-specification',
'parent_index': 0,
'children_count': 0,
'full_number_path': '1.1'},...]演算法逐步追蹤
以下用具體範例展示堆疊變化過程：
輸入資料
idx | num | level | title
----|-------|-------|---------------------------
0 | 1 | 1 | Product Feature Summary
1 | 1.1 | 2 | Jiguang specification
2 | 1.1.1 | 3 | Details
3 | 1.2 | 2 | Motherboard Block Diagram
4 | 2 | 1 | PCBA Test Plan執行步驟
Step 1: 處理 idx=0 (level=1)
lvl=1, stack=[]
→ parent_idx = None
→ stack.append((1, 0))
→ stack = [(1,0)] # lv=1, idx=0
結果: h[0]['parent_index'] = NoneStep 2: 處理 idx=1 (level=2)
lvl=2, stack=[(1,0)]
→ stack[-1][0] = 1 < 2，不 pop
→ parent_idx = 0
→ stack.append((2, 1)) # lv=2, idx=1
→ stack = [(1,0), (2,1)]
結果: h[1]['parent_index'] = 0 (父=1)Step 3: 處理 idx=2 (level=3)
lvl=3, stack=[(1,0), (2,1)]
→ stack[-1][0] = 2 < 3，不 pop
→ parent_idx = 1
→ stack.append((3, 2))
→ stack = [(1,0), (2,1), (3,2)]
結果: h[2]['parent_index'] = 1 (父=1.1)Step 4: 處理 idx=3 (level=2) 關鍵！
lvl=2, stack=[(1,0), (2,1), (3,2)]
→ while stack[-1][0] >= 2:
→ pop (3,2) # 3 >= 2
→ pop (2,1) # 2 >= 2
→ stack = [(1,0)]
→ parent_idx = 0
→ stack.append((2, 3))
→ stack = [(1,0), (2,3)]
結果: h[3]['parent_index'] = 0 (父=1)解釋：遇到 1.2 (level=2) 時，之前的 1.1.1 (level=3) 和 1.1 (level=2) 都不可能是它的父節點，必須回退到 1 (level=1)。
Step 5: 處理 idx=4 (level=1)
lvl=1, stack=[(1,0), (2,3)]
→ while stack[-1][0] >= 1:
→ pop (2,3) # 2 >= 1
→ pop (1,0) # 1 >= 1
→ stack = []
→ parent_idx = None
→ stack.append((1, 4))
→ stack = [(1,4)]
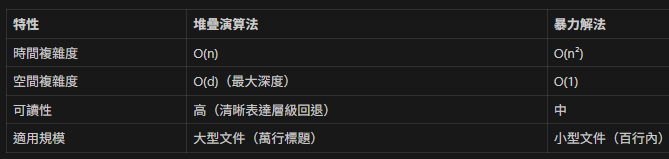
結果: h[4]['parent_index'] = None (頂層)為什麼使用堆疊？
暴力解法的問題
# 錯誤示範：O(n²) 暴力搜尋
for idx, h in enumerate(headings):
for prev_idx in range(idx-1, -1, -1):
if headings[prev_idx]['level'] < h['level']:
h['parent_index'] = prev_idx
break缺點：每個標題都要往回搜尋所有前面的標題
時間複雜度：O(n²)
堆疊解法的優勢
進階應用
- 統計子標題數量
# 在建立 parent_index 後執行
for h in headings:
parent_idx = h['parent_index']
if parent_idx is not None:
headings[parent_idx]['children_count'] += 12. 生成完整編號路徑
def get_full_path(headings, idx):
"""回傳如 '1.2.3' 的完整路徑"""
path = []
current = idx
while current is not None:
path.append(headings[current]['num'])
current = headings[current]['parent_index']
return '.'.join(reversed(path))遞迴刪除子標題
def delete_with_children(headings, idx):
"""刪除指定標題及其所有子孫標題"""
to_delete = [idx]
for i, h in enumerate(headings):
if h['parent_index'] == idx:
to_delete.extend(delete_with_children(headings, i))
return to_delete常見問題
Q1: 為什麼條件是 >= 而不是 >？
while stack and stack[-1][0] >= lvl:
stack.pop()答：因為同層級的標題不是父子關係（是兄弟關係）。例如 1.1 和 1.2 都是 level=2，1.2 的父節點不是 1.1，而是它們共同的父節點 1。
Q2: 如果 level 為 None 會怎樣？
答：程式會跳過該標題，保持 parent_index=None 且不加入堆疊（避免干擾後續判斷）。
Q3: 能否處理跳級標題（例如 1 → 1.1.1，缺 1.1）？
答：可以。演算法只依賴 level 大小關係，不要求編號連續。1.1.1 會正確找到 1 作為父節點。
測試範例
# 測試資料
test_headings = [
{'num': '1', 'level': 1, 'title': 'Chapter 1'},
{'num': '1.1', 'level': 2, 'title': 'Section 1.1'},
{'num': '1.1.1', 'level': 3, 'title': 'Subsection 1.1.1'},
{'num': '1.2', 'level': 2, 'title': 'Section 1.2'},
{'num': '2', 'level': 1, 'title': 'Chapter 2'},
]
# 執行
build_parent_child_relations(test_headings)
# 驗證
for idx, h in enumerate(test_headings):
parent = h['parent_index']
parent_title = test_headings[parent]['title'] if parent is not None else 'None'
print(f"{idx}: {h['num']} → parent={parent} ({parent_title})")
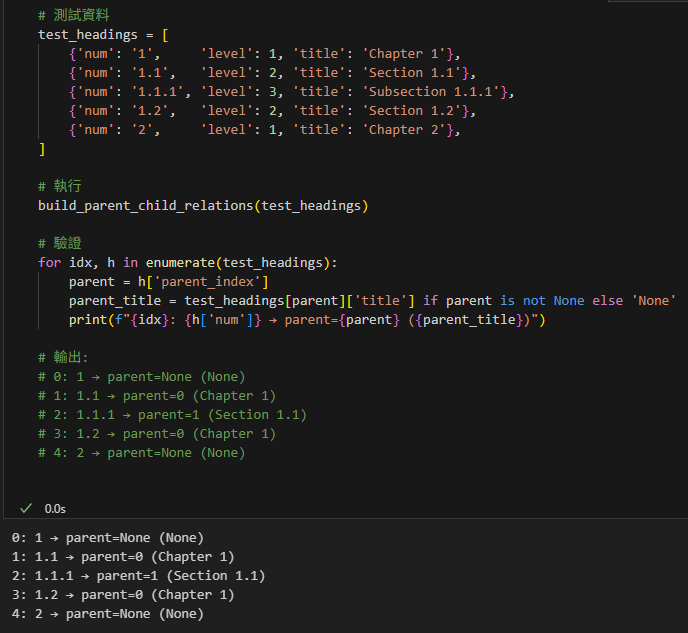
# 輸出:
# 0: 1 → parent=None (None)
# 1: 1.1 → parent=0 (Chapter 1)
# 2: 1.1.1 → parent=1 (Section 1.1)
# 3: 1.2 → parent=0 (Chapter 1)
# 4: 2 → parent=None (None)輸出:
總結
本文展示了如何用堆疊在 O(n) 時間內建立標題階層關係，核心技巧是：
- 維護有效祖先鏈：堆疊儲存潛在父節點候選
- 及時回退：遇到同級或更淺層級時彈出不合法祖先
- 單次遍歷：每個標題最多進出堆疊各一次
這種模式不僅適用於文件標題，也可用於：
- HTML DOM 樹建構
- 程式碼縮排結構解析
- 資料夾層級關係
- 任何「依序出現且帶層級」的資料
希望這篇教學能幫助你快速掌握這個經典演算法！
推薦hahow線上學習python: https://igrape.net/30afN
![Word短篇文件編輯,TQC考題110:重點摘要與評量, [(*)] 萬用字元,格式>醒目提示*2次=非醒目提示 - 儲蓄保險王](https://savingking.com.tw/wp-content/uploads/2022/03/20220322172253_75-520x245.png)
近期留言