Python機器學習: 從特徵工程到數據擬合 PolynomialFeatures 與 numpy.polyfit 的全面比較與應用; from sklearn.preprocessing import PolynomialFeatures ; poly = PolynomialFeatures( degree=2, include_bias = True) ; X_poly = poly.fit_transform(X)

導言

在數據分析與機器學習中，處理非線性數據是一項經常遇到的挑戰。這時，我們可以通過多項式擬合來建模非線性關係，或者通過特徵工程將數據升維，使模型能夠捕捉更複雜的特徵。在 Python 中，scikit-learn 的 PolynomialFeatures 和 numpy 的 polyfit 是處理多項式的兩大利器。

這篇文章將對這兩個工具進行詳細比較，並展示它們各自的應用場景與實現方式。

什麼是 PolynomialFeatures？

PolynomialFeatures 是 scikit-learn 提供的工具，專注於多項式特徵工程。它的主要功能是將輸入數據轉換為多項式特徵矩陣。這對於使用線性模型擬合非線性數據非常有用。

核心功能

1. 生成多項式特徵：將原始數據轉換成多項式形式，例如，將 [x] 轉換為 [x, x²]。
2. 支持交互項：對多維數據生成交互項，例如將 [x1, x2] 轉換為 [x1, x2, x1², x1*x2, x2²]。
3. 輔助機器學習模型：生成的多項式特徵可以作為機器學習模型的輸入，幫助捕捉非線性關係。

使用示例

以下是一個將數據轉換為二次多項式特徵的例子：

from sklearn.preprocessing import PolynomialFeatures
import numpy as np

# 原始數據
X = np.array([[1], [2], [3]])

# 初始化 PolynomialFeatures
poly = PolynomialFeatures(degree=2, include_bias=False)

# 生成多項式特徵
X_poly = poly.fit_transform(X)
print(X_poly)

輸出結果:

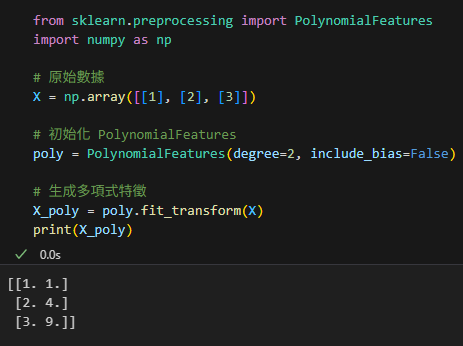
這表示：

• 第 1 列是原始數據 x。
• 第 2 列是原始數據的平方 x²。

X_poly = poly.fit_transform(X)
僅有擴展數據,
尚未得到係數跟截距

什麼是 numpy.polyfit？

numpy.polyfit 是 numpy 提供的工具，用於基於數據點擬合多項式。它可以快速計算多項式的最佳係數，適合數據擬合和趨勢建模。

核心功能

1. 計算多項式係數：根據輸入的數據點，計算符合最小二乘法的多項式係數。
2. 快速建模：適合用於單變量數據擬合，快速得到趨勢曲線公式。

使用示例

以下是一個使用 polyfit 擬合二次多項式的例子：

import numpy as np

# 原始數據
x = np.array([1, 2, 3])
y = np.array([2, 3, 5])

# 擬合二次多項式
coefficients = np.polyfit(x, y, deg=2)
print(coefficients)

輸出結果:

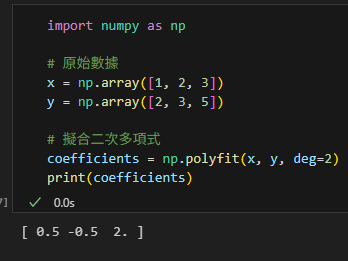
這表示擬合的多項式為：
y = 0.5x² – 0.5x + 2.0
其結果包含截距(intercept),
為最低冪次的係數
排列方式為由高到低
polyfit：fit 是“降”冪（Fit = Fall）。
sklearn：learn 是“升”冪（Learning is “rising”）。

如何用 PolynomialFeatures 實現 polyfit 的功能？

通過結合 PolynomialFeatures 和 LinearRegression，我們可以實現類似 numpy.polyfit 的效果，包括多項式係數和截距的計算。

完整流程

1. 使用 PolynomialFeatures 生成多項式特徵。
2. 使用 LinearRegression 擬合數據。
3. 獲取模型的係數和截距。

代碼示例

from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
import numpy as np

# 原始數據
x = np.array([1, 2, 3])  # 自變量
y = np.array([2, 3, 5])  # 因變量

# 轉換為 2D 數組
x = x.reshape(-1, 1)

# 1. 使用 PolynomialFeatures 生成多項式特徵
poly = PolynomialFeatures(degree=2, include_bias=False)
x_poly = poly.fit_transform(x)

# 2. 使用 LinearRegression 擬合多項式
model = LinearRegression()
model.fit(x_poly, y)

# 3. 獲取多項式係數和截距
print("係數：", model.coef_)  # [線性項係數, 二次項係數]
print("截距：", model.intercept_)

輸出:

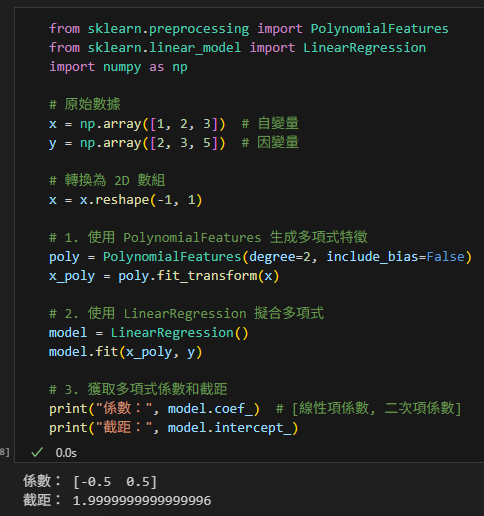
y = -0.5x + 0.5x² + 2
這與 numpy.polyfit 的結果一致
(係數排列順序相反,
且截距需要另外用.intercept_獲得)。
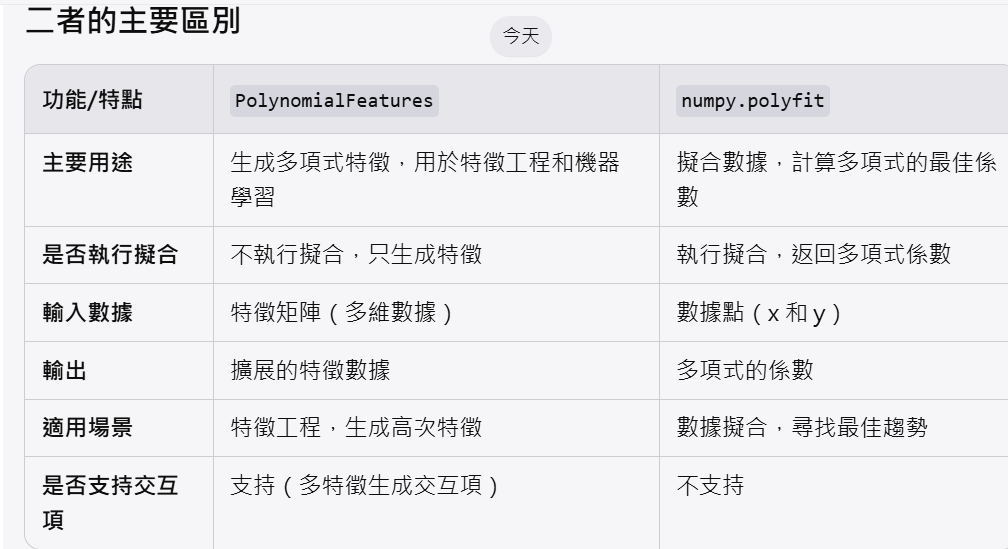
應用場景對比

PolynomialFeatures 的場景

• 特徵工程：用於生成非線性特徵，配合機器學習模型（如線性回歸）處理非線性問題。
• 多維數據：支持多維數據和交互項，擴展數據的表達能力。

numpy.polyfit 的場景

• 數據擬合：適合快速擬合單變量的多項式。
• 趨勢建模：用於分析數據點的趨勢。

結語

numpy.polyfit 則更專注於數據擬合，適合單變量的快速建模。

PolynomialFeatures 是特徵工程的利器，適合生成多維、多項式特徵，並與機器學習模型結合使用。

推薦hahow線上學習python: https://igrape.net/30afN

1. 使用 numpy.polyfit 預測新數據

numpy.polyfit 本身只用於計算多項式的係數，預測新數據需要結合 numpy.poly1d，這是一個方便的工具，可以根據多項式係數構造多項式函數。

代碼實現

import numpy as np

# 原始數據
x = np.array([1, 2, 3])
y = np.array([2, 3, 5])

# 擬合二次多項式
coefficients = np.polyfit(x, y, deg=2)

# 構造多項式函數
poly_func = np.poly1d(coefficients)

# 預測新數據
new_x = np.array([4, 5, 6])  # 新的輸入
predictions = poly_func(new_x)

print("新數據點的預測值：", predictions)

輸出:

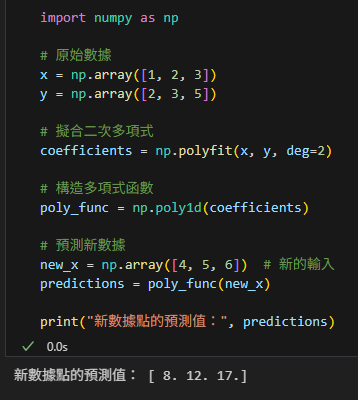
解釋

• np.polyfit 計算多項式的係數。
• np.poly1d 根據係數創建一個多項式函數，該函數可以用於任意數據點的預測。
• 預測的公式仍然是：y = 0.5x² - 0.5x + 2。

或者使用polyval:

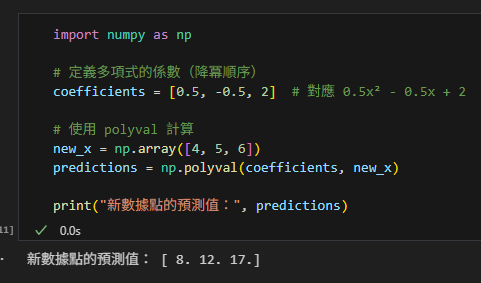
2. 使用 PolynomialFeatures + LinearRegression 預測新數據

PolynomialFeatures + LinearRegression 是基於機器學習的流程，預測新數據非常簡單，直接使用 .predict() 方法即可。

代碼實現

from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
import numpy as np

# 原始數據
x = np.array([1, 2, 3]).reshape(-1, 1)  # 自變量
y = np.array([2, 3, 5])  # 因變量

# 1. 生成二次多項式特徵
poly = PolynomialFeatures(degree=2, include_bias=False)
x_poly = poly.fit_transform(x)

# 2. 使用線性回歸擬合多項式
model = LinearRegression()
model.fit(x_poly, y)

# 3. 預測新數據
new_x = np.array([4, 5, 6]).reshape(-1, 1)  # 新的輸入數據
new_x_poly = poly.transform(new_x)  # 對新數據生成多項式特徵
predictions = model.predict(new_x_poly)

print("新數據點的預測值：", predictions)

輸出:

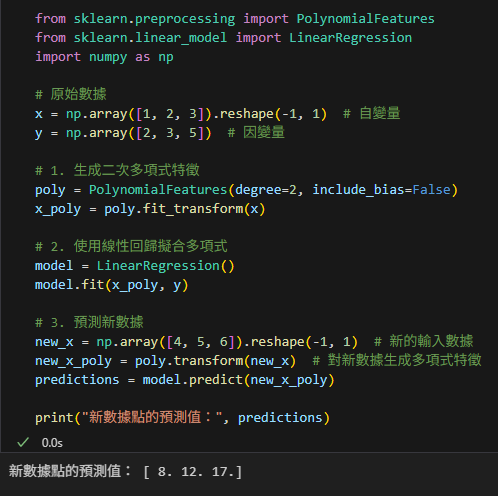
解釋

• PolynomialFeatures 對新數據進行特徵擴展，生成與訓練數據一致的多項式特徵。
• LinearRegression 的 .predict() 方法使用擬合的模型來預測新數據的結果。
• 預測的公式仍然是：y = 0.5x² - 0.5x + 2。

核心對比

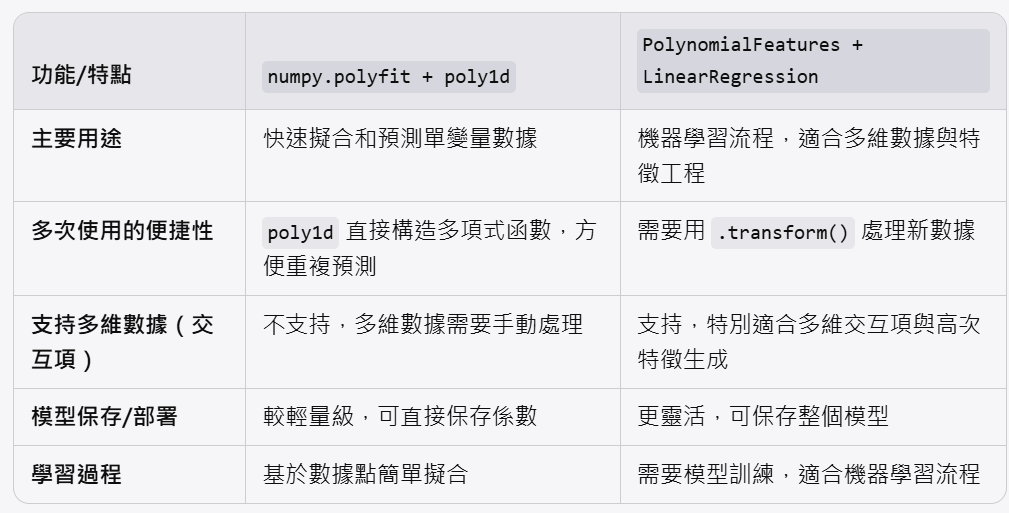
4. 適用場景

numpy.polyfit

• 適合快速處理 單變量數據，如：
  • 擬合曲線。
  • 分析數據趨勢。
  • 構造簡單的數學模型。

PolynomialFeatures + LinearRegression

• 適合處理更複雜的 機器學習任務，如：
  • 多維數據的非線性建模。
  • 特徵工程（生成交互項和高次特徵）。
  • 與其他模型（如正則化回歸）結合使用。

5. 結語

• numpy.polyfit + poly1d 是一個輕量級的工具組合，適合快速擬合和預測單變量數據，使用起來非常簡單直接。
• PolynomialFeatures + LinearRegression 提供了更靈活和擴展的能力，適合處理多維數據和更複雜的機器學習場景。

推薦hahow線上學習python: https://igrape.net/30afN